Серийные тексты: алгоритмы генерации

Основной закон информатики гласит: при полной упорядоченности сообщения, когда мы заранее точно знаем, что последует за каждым данным элементом, количество получаемой нами информации падает до нуля и сообщение расценивается как банальное, так что перестает срабатывать «восприятие».

Давайте на секунду представим гипотетическое стихотворение как систему, которая движется от одного состояния равновесия в другое. Вполне возможно проиллюстрировать точку устойчивого состояния равновесия таким примером:

Я буду называть стихотворение «заполненным» или «незаполненным», а мерой заполненности буду считать количество информации, которое в нем содержится. Если стихотворение состоит из повторяющейся бессчетное число раз буквы «а», то его «заполненность», то есть количество информации, стремится к нулю.

Мы можем дать этой системе толчок, и она придет в возмущенное движение, следствием которого будет более или менее конвенциональное стихотворение («Коты» Парщикова, например). Здесь система заполнена только наполовину.

Наконец, полностью случайный набор букв обеспечит системе полное «заполнение», и количество информации в ней достигнет своего максимального значения. Здесь достигается качественно новое состояние равновесия.

Можкт показаться, что в последнем случае стихотворение не содержит никакой информации, но это не так: ровно наоборот, оно несет максимум содержательной информации. Объясню почему это так. Если я принимаю «заполненность» того или иного текста за количество информации, которое он несет, то надо сразу оговориться, что я понимаю информацию в вероятностно-статистическом смысле, то есть так, как понимал ее сам Шеннон: это просто последовательность элементов, которыми могут быть двоичные знаки, или какие-то символы, или слова, но самое главное: они отвлечены от своей семантической стороны, от того, что они означают или как воспринимаются человеком.

По Шеннону количество информации, содержащейся в такой-то последовательности элементов, пропорционально ее оригинальности, то есть непредвиденности, непредсказуемости, но никак не смыслу. Отсюда получается, что наибольшее количество информации несет текст, все элементы которого равновероятны; что в тексте, в котором соблюдаются лишь грамматические связи, больше информации, чем в обычном осмысленном тексте, а максимальной информацией текст на естественном языке будет обладать лишь в том случае, если выбор слов чисто случайный.

Если так понимать информацию и ее ценность, то абстрактное искусство или сюрреалистический текст более информативны, нежели предметная живопись и обычная проза. Еще больше увлекательных сведений об элементарной теории информации можно найти в крайне необычной и предназначенной для гуманитариев книге французского филолога и математика Абраама Моля «Теория информации и эстетическое восприятие».

Ясно, что максимально «заполнить» текст можно самым простым путем: с помощью генератора случайных чисел, который выдаст неповторяющуюся последовательность символов. Но такой результат годится только в том случае, если приемником информации является машина, которой безразлично, что значит этот набор букв, лишь бы выполнялось условие информационной плотности и насыщенности текста. Но если в роли потребителя текста выступает человек, то он должен иметь для него какую-то эстетическую ценность, что предполагает другое решение этой задачи с другим конечным результатом. Здесь можно поставить приблизительную задачу: найти алгоритм, генерирующий текст заданного объема, в котором достигался бы максимум количества информации при связности (или хотя бы ее имитации) его элементов.

Для обеспечения наибольшего «заполнения» текста алгоритм должен развертываться на двух уровнях: в первом случае за наименьшие элементы (или гранулы) текста принимаются символы, а во втором — слова. Алгоритм, на котором я окончательно остановился, во многом отталкивается от структуры атональной или серийной музыки, которой занимались композитор Арнольд Шенберг и его ученики.

Далее следует небольшой экскурс в авангардную музыку, который необходим для того, чтобы утвердить схему моего алгоритма. Шенберг писал атональную музыку, которую в отечественном музыковедении принято называть додекафонией. Такая музыка очень структурирована и подчиняется строгим правилам композиции. В атональной музыке вводится понятие музыкального ряда, который определяется через цифровую нотацию, то есть каждому высотному классу ставится в соответствие некоторое неповторяющееся число. Для ряда-множества основной единицей является не звук, но число, его представляющее.

За основу всей музыкальной пьесы берется 12-тональная серия {C, C#, D, D#, E, F, F#, G, G#, A, A#, B}, которую можно представить как набор чисел { 0, 1, …, 11 }. В качестве базовой компоненты своего музыкального произведения композитор выбирает то или иное множество неповторяющихся чисел. Множество (9, 10, 0, 3, 4, 6, 5, 7, 8, 11, 1, 2), к примеру, используется в качестве основной компоненты (или инварианта) пьесы Шенберга «Ser­e­nade op. 24»:

Музыкальная запись серии в пьесе Шенберга «Ser­e­nade op. 24»

Здесь важно, что все цифры музыкального ряда не повторяются, то есть равновероятны. Это значит, что музыкальное произведение, построенное на основе того или иного музыкального ряда, будет содержать больше информации, нежели обычное произведение, построенное в тональной системе.

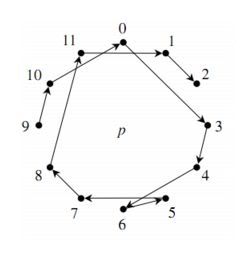
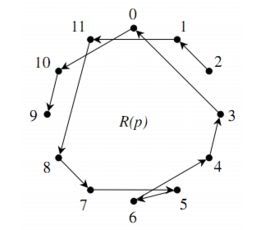
Дальше начинается самое интересное. Серийная техника использует серию (ряд звуков или чисел их представляющих) для разнообразного варьирования, транспозиций и ротаций по строгим математическим законам, и совокупность этих операций образует звуковысотную ткань произведения. Интонационный комплекс произведения, от которого зависит его вариабельность, может существовать в четырех основных формах: прима P, ракоход R, инверсия I, ракоходная инверсия IR. Для меня как для разработчика алгоритма генерации текста особый интерес представляет такая элементарная операция как ракоход, при которой звуки играются в обратном порядке.

Прима…

…ракоход…

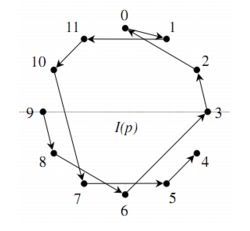
…и инверсия исходной серии
в виде круговых диаграмм

Принципы композиции серийной музыки можно распространить на написание серийных текстов или серийных стихотворений. В этом случае есть определенный класс символов, например, согласных, из которых строится конечная фраза, причем каждый символ может быть использован в этой фразе только один раз. Гласные звуки служат здесь «клеем», связующим звеном между согласными, основное правило для которых: не повторяться. Фраза может быть принята в качестве инварианта, чтобы на ее основе при помощи операции ракохода (реверса) можно было получить вторую фразу, в которой порядок следования согласных букв будет обратным по отношению к порядку следования согласных в исходной фразе. Можно ввести понятие «заикания», когда одна и та же согласная может встречаться во фразе несколько раз, но только в том случае, если каждое вхождение этой согласной во фразу строго следует друг за другом и не прерывается другими согласными.

Две полученные фразы образуют текст серийного стихотворения. Разумеется, в качестве комбинаторного материала можно использовать гласные, а не согласные. Тогда последние опять-таки будут выступать в роли «клея». Возможности такой комбинаторной техники этим далеко не исчерпываются, и параллели между музыкой и текстом можно было бы провести еще дальше.

Виви, 2011